DIMENSI
Dalam fisika dan matematika, dimensi atau matra dari suatu ruang atau objek secara informal diartikan sebagai jumlah minimal koordinat yang dibutuhkan untuk menentukan titik-titik yang ada di dalamnya. Jadi, sebuah garis memiliki dimensi karena hanya satu koordinat yang dibutuhkan untuk menentukan suatu titik di permukaannya. Permukaan seperti bidang atau permukaan suatu tabung memiliki dimensi keduanya karena dibutuhkan dua koordinat untuk menentukan titik pada permukaannya (misalnya untuk menentukan titik di permukaan dibutuhkan lintang dan bujurnya). Bagian dalam kubus, tabung bersifat tiga dimensi karena dibutuhkan tiga koordinat untuk menentukan suatu titik di dalam ruangnya.
Dibawah ini adalah sebuah gambar yang menjelaskan fisualisasi dari dimensi 0 sampai dimensi ke-4. dari gambar tersebut jelas dapat diatrik kesimpulan bahwa dimensi berikutnya adalah merupakan kumpulan dari dimensi sebelumnya yang tersusun secara teratur.
Dalam istilah fisika, dimensi merujuk pada struktur konstituen dari semua ruang (volum) dan posisinya dalam waktu (dipersepsikan sebagai dimensi skalar di sepanjang sumbu t), serta cakupan spasial objek-objek di dalamnya – struktur yang memiliki korelasi dengan konsep partikel dan medan yang berinteraksi sesuai relativitas massa dan pada dasarnya bersifat matematis. Sumbu ini atau sumbu lainnya dapat diarahkan untuk mengidentifikasi suatu titik atau struktur dalam tanggapan dan hubungannya terhadap objek lain.
Teori fisika yang mencakup unsur waktu (misalnya relativitas umum) dianggap terjadi dalam "ruang waktu" empat dimensi yang didefinisikan sebagai ruang Minkowski. Teori modern cenderung lebih "berdimensi tinggi", termasuk teori medan kuantum dan string. Ruang tetap mekanika kuantum adalah ruang fungsi berdimensi tidak terbatas. Konsep dimensi tidak dibatasi hingga benda fisik saja. Ruang berdimensi tinggi sering muncul dalam matematika dan ilmu pengetahuan atas berbagai alasan, terutama dalam bentuk ruang konfigurasi sebagaimana mekanika Lagrange atau Hamilton; keduanya adalah ruang abstrak dan terbebas dari ruang fisik yang di tempati manusia.
Para ilmuan sekarang ini baru memahami terkait dengan dimensi ke 4 saja. kemampuan untuk memfisualisasikan dimensi yang lebih tinggi sangat sulit dan rumit. Alih-alih belajar logika, ketika mengetahui ke hal yang lebih dalam maka hasil yang diperoleh adalah diluar daripada logika dan nalar manusia. Mari kita lebih lanjut mempelajari tentang dimensi-dimensi yang ada dalam geometri.
Geometri adalah cabang matematika yang bersangkutan dengan pertanyaan bentuk. Geometri muncul secara independen di sejumlah budaya awal sebagai ilmu pengetahuan praktis tentang panjang, luas, dan volume, dengan unsur-unsur dari ilmu matematika formal yang muncul di Barat sedini Thales (abad 6 SM).
ZERO DIMENSI
Dalam matematika, ruang topologi nol dimensi merupakan ruang topologi yang memiliki dimensi nol sehubungan dengan salah satu dari beberapa gagasan yang tidak setara untuk menetapkan dimensi ke ruang topologi tertentu. Ilustrasi grafis dari ruang 0 dimensi adalah sebuah titik.
Titik adalah suatu gagasan primitif yang memodelkan lokasi yang tepat di dalam ruang, serta tidak memiliki panjang, lebar, atau kedalaman. Gagasan primitif pada konteks ini berarti bahwa suatu titik tidak dapat didefinisikan dalam objek yang didefinisikan sebelumnya, dalam artian bahwa titik hanya didefinisikan dengan beberapa aksioma yang harus terpenuhi. Titik dalam matematika yang modern lebih mengacu pada suatu anggota dari suatu himpunan yang dikenal dengan sebutan ruang.
Aksioma, postulat atau asumsi adalah pernyataan yang berfungsi sebagai premis atau titik awal untuk alasan dan argumen lebih lanjut. Aksioma diartikan juga sebagai suatu pernyataan yang memuat istilah dasar dan istilah terdefinisi dan tidak berdiri sendiri dan tidak diuji kebenarannya. Akan tetapi, aksioma dalam matematika bukan berarti proposisi yang terbukti dengan sendirinya. Melainkan, suatu titik awal dari sistem logika. Misalnya, 1+1=2. Nama lain dari aksioma adalah postulat. Suatu aksioma adalah basis dari sistem logika formal yang bersama-sama dengan aturan inferensi mendefinisikan logika. Pada akhirnya aksioma merupakan sebuah pernyataan yang sudah pasti kebenarannya.
Zero dimensi adalah awal mula terciptanya suatu garis yang membentuk bangun dalam ilmu geometri, ketika kalian akan membuat suatu garis di atas kertas maka kamu akan memulai (x) menempelkan pulpen dan mulai memnggerakannya sampai akhir (y). dari menempelnya pulpen (x) dan sampai diangkatnya pulpen dari kertas (y) adalah dua bagian yang kita ilustrasikan sebagai titik. awal (x) dan akhir (y). dua titik tersebut merupakan dimensi 0 dan garis yang mencul merupakan bagian dari dimensi 1.
Dengan demikian kita mengetahui bahwa garis merupakan dimensi 1 yang terbentuk dari dua titik yaitu (titik x dan titik y), jadi adanya garis karena ada titik, lantas adanya titik karena ada apa?, munculnya titik berawal dari sebuah kebenaran mutlak penciptaannya, atau melalui syarat-syarat tertentu sehingga suatu titik muncul dan di susul dengan titik-titik lain yang akan membentuk dimensi yang lebih tinggi.
Dapat diartikan bahwa dimensi 0 adalah material yang terlampau kecil sehingga terkadang dapat dibilang sebagai hampa yang sering kita ilustrasikan dengan sebuah titik (0);
DIMENSI PERTAMA
1 dimensi atau satu matra dalam fisika dan matematika, adalah sebuah urutan dari n nomor dapat dipahami sebagai titik lokasi di ruang dimensi n. Ketika n = 1, himpunan semua lokasi tersebut disebut ruang Euclid 1-dimensi.
Dimensi 1, terdiri dari beberapa dimensi 0, yaitu garis. Jika anda membuat titik di secarik kertas yang banyak dari suatu titik ke titik lain, itu akan menjadi sebuah garis. Garis memiliki satu sifat, yaitu panjang (p). Pada dimensi satu, kita akan menemukan titik dan garis. Titik adalah sesuatu yang memiliki posisi namun tidak memiliki ukuran entah itu luas maupun volume.
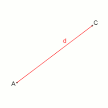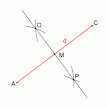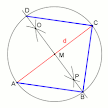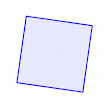
Dalam matematika, titik ditandai dengan huruf kapital. Sedangkan garis ialah kumpulan dari titik-titik yang berderet sampai pada jarak tak hingga, dan untuk membentuk sebuah garis diperlukan minimal dua titik yang dapat tarik garis lurus dari salah satu titik ke titik yang lainnya. Garis tidak memiliki luas maupun volume, namun ia dapat dihitung panjangnya. Dalam bahasa matematika, sebuag garis dilambangkan dengan huruf kecil. Di bawah ini merupakan gambar dari titik dan garis:
Dapat kita simpulkan dari uraian di atas bahwa dimensi pertama dapat difisualisasikan sebagai garis yang memiliki sifat panjang anatar satu titik dengan titik lain. semakin banyak titik maka akan semakin banyak garis yang dapat difisualisasikan yang nantinya akan membentuk sebuah bangun yang disebut dengan bangun datar 2 dimensi.
DIMENSI KEDUA (2D)
2 dimensi (biasa disingkat 2D), dua matra, atau bidang. Istilah ini biasanya digunakan dalam bidang seni, animasi, komputer dan matematika. Dimensi 2 terdiri dari beberapa dimensi 1, dan menjadi bangun datar. Jika anda lihat, sebuah persegi terdiri dari 4 garis, segitiga terdiri dari 3 garis, dan seterusnya. Sifat yang dimiliki bangun datar adalah panjang dan lebar (p,l).
Seperti yang kita ketahui pahwa dimensi dua berbentuk bidang datar, sehingga pada dimensi dua tentunya akan kita bahas hal-hal terkait bentuk bangun datar yang terdapat pada dimensi dua. Berbeda dengan dimensi satu, bangun datar pada dimensi dua memiliki ukuran berupa panjang, luas, dan keliling. Bangun datar yang biasanya dibahas pada lingkup dimensi dua antara lain segitiga, persegi, persegi panjang, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran.
Segitiga adalah poligon dengan tiga ujung dan tiga simpul. Ini adalah salah satu bentuk dasar dalam geometri. Dalam geometri Euclidean, setiap tiga titik, ketika non-collinear, menentukan segitiga unik dan sekaligus, sebuah bidang unik (yaitu ruang Euclidean dua dimensi). Dengan kata lain, hanya ada satu bidang yang mengandung segitiga itu, dan setiap segitiga terkandung dalam beberapa bidang. Jika seluruh geometri hanya bidang Euclidean, hanya ada satu bidang dan semua segitiga terkandung di dalamnya; namun, dalam ruang Euclidean berdimensi lebih tinggi, ini tidak lagi benar.
Diagram Euler dari jenis segitiga, menggunakan definisi bahwa segitiga sama kaki memiliki setidaknya 2 sisi yang sama (mis., Segitiga sama sisi sama kaki).
Persegi adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang dan memiliki empat buah sudut yang kesemuanya adalah sudut siku-siku. Bangun ini disebut juga sebagai bujur sangkar. Persegi merupakan turunan dari segi empat yang mempunyai ciri khusus keempat sisinya sama panjang dan keempat sudutnya siku-siku (90°).
a) di sebelah kiri adalah Kuadrat pada diagonal yang diberikan; b) disebelah tengah adalah Kuadrat pada panjang sisi yang diberikan, sudut kanan dengan menggunakan teorema Thales; c) disebelah kanan adalah Kontruksi pembuatan persegi.
Persegi panjang adalah bangun datar dua dimensi yang dibentuk oleh dua pasang sisi yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki empat buah sudut yang kesemuanya adalah sudut siku-siku.
Trapesium adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang.Trapesium termasuk jenis bangun datar segi empat yang mempunyai ciri khusus.
Jajar genjang atau jajaran genjang (bahasa Inggris: parallelogram) adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki dua pasang sudut yang masing-masing sama besar dengan sudut di hadapannya. Jajar genjang termasuk turunan segiempat yang mempunyai ciri khusus. Jajar genjang dengan empat rusuk yang sama panjang disebut belah ketupat.
Lingkaran adalah bentuk yang terdiri dari semua titik dalam bidang yang berjarak tertentu dari titik tertentu, pusat; ekuivalennya adalah kurva yang dilacak oleh titik yang bergerak dalam bidang sehingga jaraknya dari titik tertentu adalah konstan. Jarak antara titik mana pun dari lingkaran dan pusat disebut jari-jari. Artikel ini adalah tentang lingkaran dalam geometri Euclidean, dan, khususnya, bidang Euclidean, kecuali jika dinyatakan sebaliknya.
Secara khusus, sebuah lingkaran adalah kurva tertutup sederhana yang membagi pesawat menjadi dua wilayah: interior dan eksterior. Dalam penggunaan sehari-hari, istilah "lingkaran" dapat digunakan secara bergantian untuk merujuk pada batas gambar, atau keseluruhan gambar termasuk bagian dalamnya; dalam penggunaan teknis yang ketat, lingkaran hanyalah batas dan seluruh gambar disebut cakram.
Lingkaran juga dapat didefinisikan sebagai jenis elips khusus di mana dua fokus bertepatan dan eksentrisitasnya adalah 0, atau bentuk dua dimensi yang melingkupi area per satuan perimeter kuadrat, menggunakan kalkulus variasi.
Elips atau oval yang beraturan adalah gambar yang menyerupai lingkaran yang telah dipanjangkan ke satu arah. Elips adalah salah satu contoh dari irisan kerucut dan dapat didefinisikan sebagai lokus dari semua titik, dalam satu bidang, yang memiliki jumlah jarak yang sama dari dua titik tetap yang telah ditentukan sebelumnya (disebut fokus).
DIMENSI KETIGA (3D)
Dimensi 3 adalah dimensi dunia nyata, dan memiliki 3 sifat, yaitu panjang, lebar, dan tinggi (x, y, dan z). Seperti penjelasan sebelumnya bahwa ruang 3 dimensi tersusun atas beberapa bangun datar, seperti kubus yang membutuhkan 6 persegi. Nama dimensi ini adalah ruang.
DIMENSI KEEMPAT (4D)
Dimensi keempat dikenal sebagai waktu, dan waktu adalah sebuah garis vektor tersendiri, sering disebut timeline (t). Sebagai makhluk 3 dimensi ‘menaiki’ waktu dari masa lalu ke masa depan. Jika alam semesta ini adalah sebuah kereta yang berjalan, maka waktu adalah lintasan dari kereta tersebut. Oleh karena itu, kita sebenarnya tidak hanya hidup di dimensi ke-3, namun di gabungan ke-3 dan 4. Istilah spacetime, ini adalah tempat yang ditempati sekarang. Tanpa waktu, tidak akan bisa bergerak. Dapat dianalogikan dengan sebuah animasi/video. Di video/animasi, jika belum di-play video tersebut, hal yang dilihat adalah gambar tak bergerak, namun setelah di-play gambar itu pun bergerak. Nah, gambar itu bergerak seperti di dunia nyata, karena waktu adalah faktor yang membuat dunia ini bergerak. Lantas mengapa manusia tidak bisa pergi ke masa lalu? Walaupun ‘menaiki’ waktu, manusia tidak dapat ‘menyetir’ waktu karena manusia bukan sebuah makhluk atau entitas 4 dimensi. Misalnya jika membuat gambar di kertas, lalu kertas tersebut digerakkan di dalam gambar tersebut keliling ruangan. Gambar itu tidak dapat berbuat apa-apa karena gambar itu ada di dimensi kedua, dan ruangan adalah dimensi ke-3. Sama halnya seperti manusia yang berada di dimensi ke tiga, tidak bisa berbuat apa apa di dimensi ke-4.
Sumber :
- https://id.wikipedia.org/wiki/Dimensi#:~:text=Dalam%20fisika%20dan%20matematika%2C%20dimensi,titik%20yang%20ada%20di%20dalamnya.
- https://id.wikipedia.org/wiki/Titik_(geometri)
- https://id.wikipedia.org/wiki/Aksioma
- https://id.wikipedia.org/wiki/Geometri#:~:text=Geometri%20dalam%20dua%20dimensi%20adalah,hanya%20melibatkan%20panjang%20dan%20lebar.
- https://id.wikipedia.org/wiki/Tesseract_(geometri)
- https://id.quora.com/Dapatkah-anda-menjelaskan-apa-itu-dimensi-yang-lebih-tinggi-dari-tiga-dimensi-seperti-4-dimensi-5-dimensi-dsb-secara-sederhana-Saya-kesulitan-memahami-konsep-multidimensi-tersebut
- https://rumuspintar.com/geometri/
- https://id.wikipedia.org/wiki/Persegi
- https://id.wikipedia.org/wiki/Segitiga
















Tidak ada komentar:
Posting Komentar